Gül (matematik)

Matematikte gül veya rodonea (Yunanca gül anlamına gelen rodon kelimesinden), kutupsal koordinat sisteminde çizilmiş bir sinüs ya da kosinüs eğrisine denir. Gül eğrisi, aşağıdaki kutupsal denklemle ifade edilir:

7 yapraklı gül (k=7)

8 yapraklı gül (k=4)

Bazı rasyonel k değerlerine karşılık gelen güller (k=n/d)

$\,r=a\cos(k\theta ).$

Bu denklemde kosinüs yerine sinüs de yazılabilir, ortaya çıkacak eğri kosinüs eğrisinin π/2k radyan kadar döndürülmüş bir kopyası olacaktır. Bunun sebebi de sinüs ve kosinüs arasındaki şu ilişkidir:

$\sin(k\theta )=\cos \left(k\theta -{\frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right).$

Gül eğrisi aynı zamanda, orijinden çıkan ve sabit açısal hızla dönmekte olan bir doğrunun üzerinde sinüs/kosinüs dalgası şeklinde ileri geri hareket eden bir noktanın izleyeceği eğridir.

Denklemdeki a değeri gülün şeklini değil, bir bütün olarak büyüklüğünü (yani yaprakların uzunluğunu) etkiler.

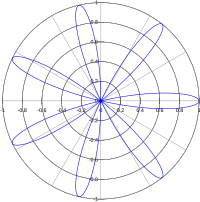
Eğer k bir tek sayı ise, gül şeklinin tamamen çizilmesi için θ'nın π uzunluğunda bir interval boyunca ilerlemesi yeterlidir ve ortaya çıkacak gül k yapraklı olacaktır. Yok eğer k bir çift sayı ise, şeklin tamamen çizilmesi için θ'nın 2π uzunluğunda bir intervalde ilerlemesi gerekir ve ortaya çıkacak gül 2k yapraklı olacaktır. Burada ilginç bir nokta şudur: Herhangi bir tek sayının iki katı kadar (2, 6, 10, 14, 18, vs.) yaprağı olan bir gül çizilemez.

Elbette k bir tam sayı olmak zorunda değildir, rasyonel ya da irrasyonel de olabilir. Eğer k bir rasyonel sayı ise, ortaya çıkan eğri topolojik anlamda kapalı ve sonlu uzunlukta olacaktır. k irrasyonel ise, eğri kapalı olmayacak ve uzunluğu sonsuz olacaktır.

Bu eğrilere gül ismini veren, 18. yüzyıl İtalyan matematikçisi Guido Grandi'dir.

Alan

Eğer k bir çift sayı ise,

$\,r=a\cos(k\theta )$

eşitliğiyle tanımlanan gülün alanı, şöyle hesaplanabilir:

$\int _{0}^{2\pi }\int _{0}^{a\cos(k\theta )}r\,drd\theta ={\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}.$

Benzer şekilde, eğer k bir tek sayı ise, gülün alanı şu olacaktır:

$\int _{0}^{\pi \,}\int _{0}^{a\cos(k\theta )}r\,drd\theta ={\frac {1}{2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}.$

Dikkat edilirse, alan formüllerinde k gözükmemektedir, yani güllerin alanları k'nın değerinden bağımsızdır. Ayrıca, çift yapraklı güllerin alanı, tek yapraklı güllerin alanının iki katıdır.

Dış bağlantılar

• MathWorld'den Gül 11 Temmuz 2007 tarihinde Wayback Machine sitesinde arşivlendi. sayfası (İngilizce)
• Girilen parametrelerle gül çizen Java uygulaması 27 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi.