Küresel kapak
Bu madde, Vikipedi biçem el kitabına uygun değildir. (Şubat 2016) |
Küresel kapak veya küresel kubbe geometride bir terimdir. Bir kürenin bir kısmı ve bir düzlem ile kesilir. Eğer düzlem kürenin merkezinden geçer, böylece kapağın yüksekliği kürenin yarıçapına eşittir, küresel kapağa bir yarıküre denir.
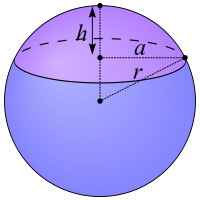
Hacim ve yüzey alanı
değiştirEğer kapağın tabanının yarıçapı ve kapağın yüksekliği ise küresel kapağın hacimi
- dir
ve küresel kapağın eğri yüzey bölgesidir
ve arası ilişki sürece ilgisizdir ve . Açıklamada mavi bölüm ayrıca küresel bir başlıktır..
Parametreler , ve bağımsız değildir:
- .
Bu bölge formülü içinde yerine konarak verilirse:
Ayrıca diyagramın üst yarıküre içinde, ve in the alt yarıküre ; bundan dolayı in ya da yarıküre ve böylece hacim için bir alternatif bağıntı
- .
Uygulamalar
değiştirburadaki tüm noktaların hacmi kesişen iki küreler r1 ve r2 yarıçaplarının en az birindedir
- [1] ,
burada
iki yalıtılmış kürenin toplamıdır ve
kesişmiş iki küresel kapakların toplamıdır. Eğer d <r1+r2 iki küre merkezleri arası uzunluk, değikenlerin eliminasyonu h1 ve h2 yoluyla [2]
Genelleştirme
değiştirDiğer katı kesitleri
değiştirküresel kubbe bir sferoidin kapalı bölgesi ile elde edilir böylece the resulting kubbe is çembersel simetrik rotasyonun bir ekseni var) ve elipsoide kubbeye benzer elipsoidten türetilir.
Hiperküresel kapak
değiştirGenel olarak, yüksekliğinin bir hiperküresel kapağın ve yarıçapı -boyutlu hacmi -boyutlu Öklidyen uzay içinde:[4] ile verilir. burada (gama fonksiyonu) ile verilir.
formül için birim n-kürenin hacim terimlerinin içinde ifade edilebilir ve hipergeometrik fonksiyon veya düzenli tamamlanmamış beta fonksiyonu as
- ,
ve bölge formülü birim n-kürenin bölgenin terimleri içinde ifade edilebilir nin bölgenin as
- ,
burada .
Ayrıca bakınız
değiştir- Daire segmenti-benzer 2D nesne.
- Kubbe (matematik)
- Katı açı-n-küre kapaklar için formül içerir
- Küresel bölüm
- Küresel sektör
- Küresel kama
Kaynakça
değiştir- ^ Connolly, Michael L. (1985). "Computation of molecular volume". J. Am. Chem. Soc. ss. 1118-1124. doi:10.1021/ja00291a006.
- ^ Pavani, R.; Ranghino, G. (1982). "A method to compute the volume of a molecule". Comput. Chem. doi:10.1016/0097-8485(82)80006-5.
- ^ Bondi, A. (1964). "van der Waals volumes and radii". J. Phys. Chem., 68. ss. 441-451. doi:10.1021/j100785a001.
- ^ Li, S. (2011). "Concise Formulas for the Area and Volume of a Hyperspherical Cap". Asian J. Math. Stat. 4 (1): 66–70. doi:10.3923/ajms.2011.66.70
- Richmond, Timothy J. (1984). "Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect". J. Molec. Biol. 178 (1). ss. 63-89. doi:10.1016/0022-2836(84)90231-6.
- Lustig, Rolf (1986). "Geometry of four hard fused spheres in an arbitrary spatial configuration". Mol. Phys. 59 (2). ss. 195-207. Bibcode:1986MolPh..59..195L. doi:10.1080/00268978600102011.
- Gibson, K. D.; Scheraga, Harold A. (1987). "Volume of the intersection of three spheres of unequal size: a simplified formula". J. Phys. Chem. 91 (15). ss. 4121-4122.
- Gibson, K. D.; Scheraga, Harold A. (1987). "Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii". Mol. Phys. 62 (5). ss. 1247-1265. Bibcode:1987MolPh..62.1247G. doi:10.1080/00268978700102951.
- Petitjean, Michel (1994). "On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects". Int. J. Quant. Chem. 15 (5). ss. 507-523.
- Grant, J. A.; Pickup, B. T. (1995). "A Gaussian description of molecular shape". J. Phys. Chem. 99 (11). ss. 3503-3510. doi:10.1021/j100011a016.
- Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). "ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations". Comp. Phys. Commun. Cilt 165. ss. 59-96. Bibcode:2005CoPhC.165...59B. doi:10.1016/j.cpc.2004.08.002.
- Li, S. (2011). "Concise Formulas for the Area and Volume of a Hyperspherical Cap". Asian J. Math. Stat. 4 (1). ss. 66-70. doi:10.3923/ajms.2011.66.70..
Dış bağlantılar
değiştir- Şablon:MatematikWorld, derivation and some additional formulas
- Online calculator for spherical cap volume and area 9 Temmuz 2020 tarihinde Wayback Machine sitesinde arşivlendi.
- Summary of spherical formulas 3 Şubat 2014 tarihinde Wayback Machine sitesinde arşivlendi.