Parabol

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Paraboller sanılanın aksine fonksiyon değillerdir çünkü y²=x gibi yatay veya eğik paraboller de bulunmaktadır. Parabollerin bazıları, y=ax²+bx+c şeklindeki ikinci dereceden polinomların grafikleri şeklindedir.

Parabol üzerinde alınan herhangi bir noktanın(P1, P2, P3) doğrultmana(L) ve odak noktasına(F) olan uzaklıkları eşittir.

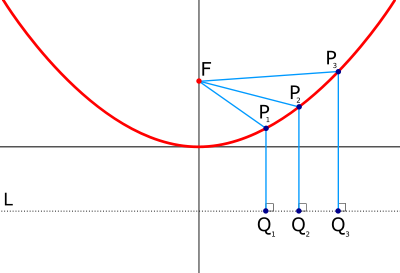
Terimler

• Sabit F noktasına parabolün odağı, d doğrusuna da parabolün doğrultmanı denir.
• F noktasından geçip d doğrusuna dik olan doğruya parabol ekseni denir. Parabol, bu eksene göre simetrik iki koldan ibarettir. Parabol üzerindeki her noktanın odak noktasına olan uzaklığı, doğrultmana olan uzaklığına eşittir.
• Parabole ait herhangi iki noktayı birleştiren doğru parçasına kiriş denir.
• Odaktan geçen parabol eksenine dik olan kirişin yarısına parametre denir ve "p" ile gösterilir.
• Parabolün ekseni kestiği noktaya tepe noktası adı verilir.

Denklemler

y=x² parabolü

Kartezyen koordinat sisteminde bir parabolün denklemi:

$y=ax^{2}+bx+c$ şeklindedir.

Burada a, parabolün yönünü gösterir. Eğer a>0 ise parabolün kolları yukarı doğrudur, eğer a<0 ise aşağı doğrudur. c değeri parabolün y ekseniyle kesiştiği yerdir.

Tepe noktası

Tepe noktasının koordinatları "T"(r, k) olarak gösterilir. Tepe noktasında fonksiyonun eğimi 0 olduğundan türev alınıp sıfıra eşitlenirse,

$x_{1}+x_{2}={\frac {-b}{a}}$

${\frac {x_{1}+x_{2}}{2}}={\frac {-b}{2a}}$(orta nokta,simetri ekseni vs.)

$r={\frac {-b}{2a}}$,

$k=f(r)={\frac {4ac-b^{2}}{4a}}$ bulunur. Ve denklem,

$y=f(x)=a(x-r)^{2}+k$ şeklinde yeniden yazılabilir. Aynı zamanda x=r doğrusu parabolün simetri ekseni olur.

Ayrıca bakınız

• Matematiksel şekillerin listesi
• Katener
• Elips
• Hiperbol
• Kubbe
• Parabolik yansıtıcı
• Parabolik kısmi diferansiyel denklem
• Parabloid
• 2. derece denklemler