Durgun kütle
Değişmez kütle, durgun kütle,[1] gerçek kütle, tam kütle ya da sınır sistemleri durumunda basitce kütle, bir objenin veya Lorentz dönüşümlerine göre tüm referans çerçevelerinde aynı olan objelerin sisteminin toplam enerji ve momentum karakteridir. Eğer momentum çerçevesinin bir merkezi sistemde oluşuyorsa, sistemin değişmez kütlesi toplam enerjinin ışık hızının karesine bölümüyle bulunur. Diğer referans çerçevelerinde, sistemin enerjisi artar yalnız sistemin momentumu bundan çıkarılmıştır, yani değişmez kütle aynı kalır.
4-momentumu boş vektör olan (örneğin tek bir foton ya da tam olarak aynı yönde hareket eden fotonlar) sistemler sıfır değişmez kütleye sahiptir ve kütlesiz olarak değerlendirilirler. Işık hızından hızlı hareket eden fiziksel bir obje veya parçacık uzay tarzı 4-momentuma sahip olabilir (hipotetik takyon gibi) ve onlar mevcut görünmez. Her zaman tarzı 4-momentum, momentumun (3 boyutlu) 0 olduğu yani momentum çerçevesinin merkezinde olan bir referans çerçevesi ele alır. Bu durumda değişmez kütle pozitiftir ve durgun kütleyi ima eder.
Sistemdeki objeler göreceli hareket halindeyse, değişmez kütle tüm objelerin durgun kütlelerinin toplamından farklıdır. Bu ayrıca sistemin toplam enerjisinin c2 ye bölümüne eşittir. Kütle tanımı hakkında tanımlar için bakınız (kütle-enerji eşitliği). Sistemlerin kütlelerinin tüm sistemin momentumunun 0 olduğu bir momentum çerçevesinde bir ağırlık veya kütle ölçer tarafından ölçülmesi gerektiğinden, böyle bir ölçek daima sistemin değişmez kütlesini ölçer. ((Örneğin, bir şişe gazdaki moleküllerin kinetik enerjisini değişmez kütlenin bir kısmı olarak ölçer ve kalan kısmı da durgun kütle olarak ölçer. Aynısı sistemdeki enerjilerine göre sisteme değişmez kütle ve durgun kütle ekleyen ağırlıksız maddeler için de doğrudur.
Büyük izole bir sistem için, sistemin küte merkezi bir doğru boyunca subliminal bir hızla(sisteme bakmak için kullanılanreferans çerçevesine bağımlı bir hızla). Böylece, daima onunla birlikte hareket eden bir gözlemci yerleştirilebilir. Momentum çerçevesinin merkezi olan bu çerçevede, toplam momentum 0'dır ve eğer sistem sınırli bir sistemse (bir şişe gaz gibi) bir bütün olarak durmuş olarak düşünülebilir. Bu şartlar altında oluşan çerçevede sistemin değişmez kütlesi toplam enerjisinin c2 ye bölümüne eşittir. (0-momentum çerçevesinde). Momentum çerçevesinin merkezindeki bu toplam enerji, değişen durgun çerçevelerden değişen izleyiciler tarafından sistemin sahip olduğu görülen minimum enerjidir.
Yukardaki sebep için not ediniz, tek yönde ilerleyen ışık ışınları ve tek fotonlar için böyle bir durgun çerçeve mevcut değildir. Oysa iki veya daha fazla foton farklı yönlerde hareket ettiğinde bir kütle merkezi çerçevesi oluşur (veya sistem sınırlıysa durgun çerçeve). Böylece, farklı yönlerde hareket eden çoklu foton sistemlerinin kütlesi pozitiftir yani her foton için olmasa dahi sistem için değişmez kütle mevcuttur.
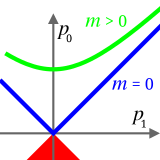
Durgun kütlelerin toplamı
değiştirDeğişmez kütle momentum çerçevesinin merkezinde bulunan tüm kinetik ve potansiyel enerji yığınını içerdiği için, sistemin değişmez kütlesi genellikle ayrı bileşenlerin durgun kütlelerinin toplamından daha fazladır. Örneğin, sistemin değişmez kütlesine pozitif etki ettikleri halde tek fotonların durgun kütle ve değişmez kütleleri sıfırdır. Bu sebepten ötürü, değişmez kütle genel olarak toplamsal bir değer değildir. (sistemdeki kinetik veya potansiyel enerjiye sahip olmayan büyük parçacıkların toplam kütle için toplanabildiği birkaç nadir durumda olabilir).
İki gövdeli sistemin basit halini düşünelim, obje A durgun haldeki diğer bir obje B' ye doğru hareket eder. (herhangi bir özel referans çerçevesinde). Bu 2 gövdeli sistemin değişmez kütlesi durgun kütle toplamından (objelerin durgun haldeki kütleleri toplamı) farklıdır. Aynı sistemi net momentumun 0 olduğu momentum çerçeve merkezinden değerlendirsek dahi, sistemin değişmez kütlesinin değeri içindeki parçacıkların durgun kütlelerinin toplamına eşit değildir.
Parçacıkların kinetik enerjisi ve güç alanlarının potansiyel enerjisi toplam enerjiyi parçacıkların durgun kütlelerinin toplamının üstüne çıkarır ve tüm terimler birleşerek sistemin değişmez kütlesine katılır. Parçacık kinetik enerjilerinin toplamı momentum çerçevesindeki çok küçük bir gözlemci tarafından hesaplanır. (tekrar, eğer sistem sınırlıysa ‘durgun çerçeve’ diye adlandırılır).
Ayrıca, parçacıklar sık sık negatif (muhtemelen) bir etkileşim potansiyel enerjisi veren bir veya daha fazla temel kuvvet ile etkileşir.
İzole büyük bir sistem için Büyük izole bir sistem için, sistemin küte merkezi bir doğru boyunca subliminal bir hızla hareket eder. Bu yüzden daima bir gözlemci onunla hareket etmek üzere yerleştirilebilir. Bu merkez momentum çerçevesinde, toplam momentum sıfırdır ve sistem eğer sınırlıysa bir bütün halinde durgun olarak değerlendirilebilir (bir şişe gaz gibi). Bu daima oluşan çerçevede, sistemin değişmez kütlesi toplam enerjinin ışık hızının karesine (c2) bölümüne(0- momentum çerçevesinde) eşittir.
Parçacık fiziğinde tanımlandığı gibi
değiştirParçacık fiziğinde, değişmez kütle m0 parçacığın durgun çerçevedeki kütlesine eşittir ve parçacığın enerjisi E ve her çerçevede ölçülen momentumu p ile enerji-momentum ilişkisinden hesaplanabilir:
Veya c=1 olan doğal birimlerde,
Değişmez kütle herreferans çerçevesinde (ayrıca özel izafiyete bakınız) aynıdır. Bu eşitlik der ki değişmez kütle uzay ve zaman ölçüleri için değişik bir anlayışı olan Pythagorian teoreminin izafi bir versiyonu kullanılarak hesaplanan 4-vektörün (E, p) sözde Euclidian uzunluğudur. Bu uzunluk 4 boyutta Lorentz artış ve dönmeleri altında muhafaza edilir, tıpkı sıradan bir vektör uzunluğunun dönmelerde muhafaza edildiği gibi. Kuantum teorisinde değişmez kütle basit bir parçacık için rölativistik Dirac eşitliğinde bir parametredir. Dirac kuantum operatörü parçacık 4-momentum vektörüne karşılık gelir.
Değişmez kütle ayrışma süresince korunan değerlerle belirlendiğinden, ayrı ürünlerin enerji ve momentumları kullanılarak hesaplanan değişmez kütlebaştaki parçacığın değişmez kütlesine eşittir. Parçacık sisteminin kütlesi bu genel formulle hesaplanabilir:
- parçacık sisteminin değişmez kütlesi, ayrışan parçacığın kütlesine eşit,
- parçacıkların enerjileri toplamı
- parçacıkların momentumlarının vektörel toplamı(momentlerin hem yön hem büyüklüğünü içerir)
Değişmez kütle terimi ayrıca inelastik saçılma deneyleri için de kullanılır. Toplam gelen enerjinin tespit edilen enerjiden büyük olduğu inelastik bir reaksiyonda, (deneyde çıkan tüm parçacıklar tespit edilmemiştir) değişmez kütle (kayıp kütle olarak da bilinir) reaksiyonun W si şu şekilde tanımlanır (temel birimlerle):
Eğer deney sırasında tespit edilmeyen baskın bir parçacık varsa, değişmez kütlenin grafiği eksik kütlenin yerine gelince bariz bir zirve gösterir.
Bir yöndeki momentumun ölçülemediği durumlarda (örneğin varlığı kayıp enerjiye dayanan nötrinolar) çaprazlama Kütle kullanılır.
Örnek: 2 parçacığın çarpışması
değiştirİki parçacığın çarpışmasında değişmez kütlenin karesi (doğal birimlerle):
Kütlesiz parçacıklar
değiştirMomentleri bir açısı oluşturan 2 kütlesiz parçacıktan oluşan sistemin değişmez kütlesi kullanışlı bir gösterime sahiptir:
Çarpıştırıcı Deneyleri
değiştirParçacık çarpıştırıcısı deneylerinde sık sık parçacıkların açısal pozisyonları yönsel açı ye ve pseudorapidity . ye göre tanımlanır. Çapraz momentuma ek olarak, , genelde ölçülür.Parçacıkların kütlesiz olduğu durumda veya fazlasıyla relativistik ( ,) olduğunda değişmez kütle şöyle olur:
Durgun enerji
değiştirBir parçacığın durgun enerjisi şu şekilde tanımlanmıştır:
- ,
c ışığın boşluktaki hızıdır.[2] Genel olarak yalnızca enerjideki farklar fiziksel önem arz eder.[3]
Durgun enerji kavramı özel izafiyet teorisini takip eder ve Einstein'ın enerji ve kütle arasındaki meşhur sonucuna götürür. (Buraya da bakınız E=mc^2)
Diğer taraftan, eşdeğer Dirac değişmez durgun enerji konsepti geometrik birleşik teorideki kütlenin tek tanımının bir parçası olarak bir geometrik madde akımı ve genelleştirilmiş potansiyele[4] karşılık gelen öz enerji açısından tanımlanabilir.
Ayrıca bakınız
değiştirKaynakça
değiştir- ^ Physics for Scientists and Engineers, Volume 2, page 1073 2 Aralık 2016 tarihinde Wayback Machine sitesinde arşivlendi. - Lawrence S. Lerner - Science - 1997
- ^ "Arşivlenmiş kopya" (PDF). 23 Haziran 2015 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 13 Mayıs 2016.
- ^ Modell, Michael; Robert C. Reid (1974). Thermodynamics and Its Applications. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-914861-2.
- ^ González-Martín, Gustavo R. (1994). "A geometric definition of mass". Gen. Rel. and Grav. Cilt 26. s. 1177. Bibcode:1994GReGr..26.1177G. doi:10.1007/BF02106710.[ölü/kırık bağlantı]
Konuyla ilgili yayınlar
değiştir- Landau, L. D., Lifshitz, E. M. (1975). Klasik Teori Alanları: 4. gözden geçirilmiş İngilizce Sürüm: Kuramsal Fizik, Vol. 2. Butterworth Heinemann. ISBN 0-7506-2768-9. CS1 bakım: Birden çok ad: yazarlar listesi (bağlantı)
- Halzen, Francis; Martin, Alan (1984). Kuark ve Lepton: Bir Giriş Dersi Modern Parçacık Fiziği. John Wiley & Sons. ISBN 0-471-88741-2. CS1 bakım: Birden çok ad: yazarlar listesi (bağlantı)