Trigonometrik integral

Matematikte, trigonometrik integraller trigonometrik fonksiyonları içeren temel olmayan integrallerin ailesidir.

Karmaşık düzlemde integral kosinüs. Negatif reel eksen boyunca dal kesimine dikkat edin.

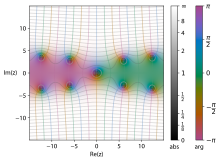
Sinüs integrali

0 \leq x \leq 8 π

için Si(x) grafiği.

Karmaşık düzlemde kosinüs integral fonksiyonu Ci(z)'nin

-2-2i

ile

2+2i

arasında Mathematica 13.1 ComplexPlot3D fonksiyonu ile oluşturulan renklerle çizimi

Farklı sinüs integral tanımları şunlardır: $\operatorname {Si} (x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt$ $\operatorname {si} (x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt~.$

${\frac {\sin(t)}{t}}$ integralinin sinc fonksiyonu ve aynı zamanda sıfırıncı küresel Bessel fonksiyonu olduğuna dikkat edin.

Çünkü $sinc$ bir çift tam fonksiyon (holomorfik tüm karmaşık düzlem üzerinde), $Si$ tamdır, tektir ve tanımındaki integral, uç noktaları birleştiren herhangi bir yol boyunca alınabilir.

Tanım olarak $Si(x)$ , $sin x / x$ 'in $x = 0$ 'da değeri sıfır olan ters türevidir ve $si(x)$ ise $x = \infty$ 'da değeri sıfır olan ters türevidir. Aralarındaki fark Dirichlet integrali tarafından verilir, $\operatorname {Si} (x)-\operatorname {si} (x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}}\quad {\text{ veya }}\quad \operatorname {Si} (x)={\frac {\pi }{2}}+\operatorname {si} (x)~.$

Sinyal işlemede, sinüs integralinin salınımları sinc filtresi kullanıldığında aşırı salınım ve halkasal bozulmaya ve alçak geçiren filtre olarak kesilmiş bir sinc filtresi kullanıldığında frekans etki alanı bozulmaya neden olur.

Bununla ilgili Gibbs fenomeni vardır: Sinüs integrali, sinc fonksiyonunun Heaviside basamak fonksiyonu ile konvolüsyonu olarak kabul edilirse, bu Gibbs fenomeninin nedeni olan Fourier serisinin kesilmesine karşılık gelir.

Kosinüs integrali

0 <

x

≤ 8

π

için

Ci(x)

grafiği.

Farklı kosinüs integral tanımları şunlardır: $\operatorname {Cin} (x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt~,$ $\operatorname {Ci} (x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt=\gamma +\ln x-\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt\qquad ~\left|\operatorname {Arg} (x)\right|<\pi ~{\text{ için }},$

burada $γ \approx 0,57721566 ...$ Euler-Mascheroni sabitidir. Bazı metinlerde $Ci$ yerine $ci$ kullanılır.

$Ci(x)$ , $cos x / x$ ( $x\to \infty$ sıfıra eşit olan) ters türevidir. Bu iki tanım,

$\operatorname {Ci} (x)=\gamma +\ln x-\operatorname {Cin} (x)~$

ile ilişkilidir. $Cin$ bir çift, tam fonksiyondur. Bu nedenle, bazı metinler $Cin$ 'i birincil fonksiyon olarak ele alır ve $Ci$ 'yi $Cin$ cinsinden türetir.

Hiperbolik sinüs integrali

Hiperbolik sinüs integrali şu şekilde tanımlanır:

$\operatorname {Shi} (x)=\int _{0}^{x}{\frac {\sinh(t)}{t}}\,dt.$

Sıradan sinüs integrali ile şu şekilde ilişkilidir:

$\operatorname {Si} (ix)=i\operatorname {Shi} (x).$

Hiperbolik kosinüs integral fonksiyonu Chi(z)'nin karmaşık düzlemde

-2-2i

ile

2+2i

arasında Mathematica 13.1 ComplexPlot3D fonksiyonu ile oluşturulan renklerle çizimi

Hiperbolik kosinüs integrali

Hiperbolik kosinüs integrali şöyledir:

$\operatorname {Chi} (x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt\qquad ~\left|\operatorname {Arg} (x)\right|<\pi ~{\text{ için }}~,$

burada $\gamma$ Euler-Mascheroni sabitidir.

Aşağıdaki seri açılımına sahiptir:

$\operatorname {Chi} (x)=\gamma +\ln(x)+{\frac {x^{2}}{4}}+{\frac {x^{4}}{96}}+{\frac {x^{6}}{4320}}+{\frac {x^{8}}{322560}}+{\frac {x^{10}}{36288000}}+O(x^{12}).$

Yardımcı fonksiyonlar

Trigonometrik integraller, "yardımcı fonksiyonlar" olarak adlandırılan terimlerle anlaşılabilir.

${\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}$

Bu fonksiyonlar kullanılarak trigonometrik integraller aşağıdaki gibi yeniden ifade edilebilir (bkz. Abramowitz & Stegun, s. 232)

${\begin{array}{rcl}{\frac {\pi }{2}}-\operatorname {Si} (x)=-\operatorname {si} (x)&=&f(x)\cos(x)+g(x)\sin(x)~,\qquad {\text{ ve }}\\\operatorname {Ci} (x)&=&f(x)\sin(x)-g(x)\cos(x)~.\\\end{array}}$

Nielsen sarmalı

$si , ci$ parametrik grafiği ile oluşturulan spiral, Nielsen spirali olarak bilinir.

$x(t)=a\times \operatorname {ci} (t)$ $y(t)=a\times \operatorname {si} (t)$

Sarmal, Fresnel integrali ve Euler spirali ile yakından ilişkilidir. Nielsen spiralinin görüntü işleme, yol ve iz yapımı ve diğer alanlarda uygulamaları vardır.^[1]

Açılım

Trigonometrik integrallerin değerlendirilmesi için argümanın aralığına bağlı olarak çeşitli açılımlar kullanılabilir.

Asimptotik seri (büyük argüman için)

$\operatorname {Si} (x)\sim {\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)$ $\operatorname {Ci} (x)\sim {\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)~.$

Bu seriler asimptotik ve ıraksaktır, ancak $ℜ(x) ≫ 1$ değerinde tahminler ve hatta kesin değerlendirme için kullanılabilir.

Yakınsak seriler

$\operatorname {Si} (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots$ $\operatorname {Ci} (x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots$

Bu seriler herhangi bir kompleks $x$ değerinde yakınsaktır, ancak $| x | ≫ 1$ için seri başlangıçta yavaş yakınsayacak ve yüksek hassasiyet için birçok terim gerektirecektir.

Seri açılımının türetilmesi

Sinüsün Maclaurin serisi açılımından: $\sin \,x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-{\frac {x^{11}}{11!}}+\cdots$

${\frac {\sin \,x}{x}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+{\frac {x^{8}}{9!}}-{\frac {x^{10}}{11!}}+\cdots$

$\therefore \int {\frac {\sin \,x}{x}}dx=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+{\frac {x^{9}}{9!\cdot 9}}-{\frac {x^{11}}{11!\cdot 11}}+\cdots$

Sanal argümanın üstel integral ile ilişki

$\operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}\,dt\qquad ~{\text{ for }}~\Re (z)\geq 0$

fonksiyonu üstel integral olarak adlandırılır. Bu integral, $Si$ ve $Ci$ ile yakından ilişkilidir;

$\operatorname {E} _{1}(ix)=i\left(-{\frac {\pi }{2}}+\operatorname {Si} (x)\right)-\operatorname {Ci} (x)=i\operatorname {si} (x)-\operatorname {ci} (x)\qquad ~{\text{ for }}~x>0~.$

İlgili her bir fonksiyon, argümanın negatif değerlerindeki kesim dışında analitik olduğundan, bağıntının geçerlilik alanı genişletilmelidir (Bu aralığın dışında, $π$ 'nin tam sayı çarpanları olan ek terimler ifadede görünür).

Genelleştirilmiş integro-üstel fonksiyonun sanal argümanının durumları şunlardır:

$\int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,$ ki bu da, $\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i\left(\gamma +\ln a\right)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}~.$ ifadesinin gerçek kısmıdır. Benzer şekilde, $\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.$

Etkin değerlendirme

Yakınsak Taylor serilerinin Padé yaklaşımları, küçük argümanlar için fonksiyonları değerlendirmenin etkili bir yolunu sağlar. Rowe ve diğerleri (2015)^[2] tarafından verilen aşağıdaki formüller, $0 \leq x \leq 4$ için $10 -16$ 'dan daha doğrudur,

${\begin{array}{rcl}\operatorname {Si} (x)&\approx &x\cdot \left({\frac {\begin{array}{l}1-4.54393409816329991\cdot 10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{-10}\cdot x^{10}+7.08240282274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}}\right)\\&~&\\\operatorname {Ci} (x)&\approx &\gamma +\ln(x)+\\&&x^{2}\cdot \left({\frac {\begin{array}{l}-0.25+7.51851524438898291\cdot 10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\\end{array}}}\right)\end{array}}$

İntegraller, yardımcı fonksiyonlar aracılığıyla dolaylı olarak değerlendirilebilir. $f(x)$ ve $g(x)$ ile tanımlanır.

$\operatorname {Si} (x)={\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)$		$\operatorname {Ci} (x)=f(x)\sin(x)-g(x)\cos(x)$
veya eşdeğer olarak
$f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)+\operatorname {Ci} (x)\sin(x)$		$g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)-\operatorname {Ci} (x)\cos(x)$

$x\geq 4$ için aşağıda verilen Padé rasyonel fonksiyonları $f(x)$ ve $g(x)$ 'e 10⁻¹⁶'dan daha az hata ile yaklaşır:^[2]

${\begin{array}{rcl}f(x)&\approx &{\dfrac {1}{x}}\cdot \left({\frac {\begin{array}{l}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{-10}+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\&&\\g(x)&\approx &{\dfrac {1}{x^{2}}}\cdot \left({\frac {\begin{array}{l}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{-10}+1.09049528450362786\cdot 10^{12}\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}$

Ayrıca bakınız

Kaynakça

^ Gray (1993). Modern Differential Geometry of Curves and Surfaces. Boca Raton. ss. 119.
^ ^a ^b Rowe, B.; ve diğerleri. (2015). "GALSIM: The modular galaxy image simulation toolkit". Astronomy and Computing. Cilt 10. s. 121. arXiv:1407.7676 $2. Bibcode:2015A&C....10..121R. doi:10.1016/j.ascom.2015.02.002.

Abramowitz, Milton; Stegun, Irene Ann, (Ed.) (1983) [Haziran 1964]. "Chapter 5". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Düzeltmelerle birlikte 10. orijinal baskının ek düzeltmelerle birlikte 9. yeniden baskısı (Aralık 1972); 1. bas.). Washington D.C., USA; New York, USA: United States Department of Commerce, Ulusal Standartlar ve Teknoloji Enstitüsü; Dover Publications. s. 231. ISBN 0-486-61272-4. LCCN 64-60036. MR 0167642. ISBN 978-0-486-61272-0. LCCN-6512253-{{{3}}}.

Konuyla ilgili okumalar

Mathar, R.J. (2009). "Numerical evaluation of the oscillatory integral over exp(i $π$ x)·x^1/x between 1 and ∞". Appendix B. arXiv:0912.3844 $2.
Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 6.8.2 – Cosine and Sine Integrals". Numerical Recipes: The Art of Scientific Computing. 3rd. New York: Cambridge University Press. ISBN 978-0-521-88068-8.
Sloughter, Dan. "Sine Integral Taylor series proof" (PDF). Difference Equations to Differential Equations.
Temme, N.M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals", Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (Ed.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248 .

Dış bağlantılar

Eric W. Weisstein, Sine Integral (MathWorld)
Hazewinkel, Michiel, (Ed.) (2001), "Integral sine", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
Hazewinkel, Michiel, (Ed.) (2001), "Integral cosine", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104

[1] Gray (1993). Modern Differential Geometry of Curves and Surfaces. Boca Raton. ss. 119.

[RoweEtAl2015-2] Rowe, B.; ve diğerleri. (2015). "GALSIM: The modular galaxy image simulation toolkit". Astronomy and Computing. Cilt 10. s. 121. arXiv:1407.7676 $2. Bibcode:2015A&C....10..121R. doi:10.1016/j.ascom.2015.02.002.

[1]

[2]