Çap

Matematiğin bir alt dalı olan geometride, bir çemberin, dairenin ya da kürenin çapı, çemberin, dairenin ya da kürenin merkezinden geçen ve uç noktaları dairenin ya da kürenin en dışardaki sınır noktalarında bulunan herhangi bir düz doğru parçasıdır. Ayrıca, çap, çemberin, dairenin veya kürenin en uzun kirişi olarak da tanımlanabilir. Çap kavramı, ayrıca, bu matematiksel nesneler ya da kümeler haricindeki kümeler için de kullanılabilir.

Bir çember; m = merkez, d = çap, r = yarıçap

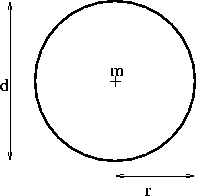
Çember, daire ya da küre gibi geometrik bir nesnenin merkezinden geçen sonsuz sayıda çap olacağı için bu tür geometrik şekillerin doğru parçası anlamında tek bir çapı yoktur. Ancak, modern kullanımda, bir çemberin, dairenin ya da kürenin çapının uzunluğuna da çap denir. Bu tür merkezlerine göre bakışımlı geometrik nesneler için, doğru parçası anlamındaki çapların uzunluğu aynıdır ve kökü Antik Yunan diline dayanan διάμετρος (diametros) teriminden esinlenerek bu uzunluk $d$ ile gösterilir.

Bir çember, daire veya kürenin merkezinden en dışarıdaki sınır noktalarına kadar olan doğru parçalarından herhangi biri yarıçap adlandırılır. Benzer bir şekilde, yarıçap terimi de modern kullanımda yarıçapı tanımlayan doğru parçalarının uzunluğu anlamına gelir. Yani, bir çapın uzunluğunun yarısına yarıçap denir ve Latince radius teriminden esinlenerek $r$ ile gösterilir. O zaman,

$d=2r\qquad {\text{veya buna denk olarak}}\qquad r={\frac {d}{2}}$

olur.

Çizimi

Bir uzunluk pergeli ve cetvel yardımıyla istenilen çap uzunluğuna sahip bir çember ya da daire ve de çapın gösterimi çizilebilir. Pergelin sabit bacağındaki iğnesi istenilen noktaya buranın çemberin ya da dairenin merkezi olacağı düşünülerek konulur. Bu noktadan cetvel ile yarıçapın uzunluğu kadar ilerideki bir nokta işaretlenir ve pergelin hareketli bacağı buraya konulur. Bundan sonra pergelin hareketli bacağı döndürülerek çember elde edilir. Cetvel yardımıyla, uç noktaları çizilen çember üzerinde olan ve merkezden geçen bir doğru parçası çizilir. Böylece, çember ve çap çizilmiş olur.

Eğer bir çember merkezi bilinmeden verilmişse, çapı çizebimek için, herhangi bir kirişin belli bir çap tarafından dik kesilip tam ikiye bölüneceği bilgisi kullanılır. O zaman, ilk adım olarak, bir gönye ya da cetvel aracılığıyla herhangi bir kiriş çizilir. Sonra bu kirişin boyu ölçülerek kirişin orta noktası bulunur. Gönyenin bir kenarının bu ortadan noktadan başlayarak kirişin üzerinde kalması sağlandıktan sonra diğer dik kenar yardımıyla kirişe dik bir çizgi çekilir. Bu çizgi ya cetvel ya da gönye yardımıyla uzatılarak eski kirişe dik yeni bir kiriş yapılır. Bu yeni kiriş, çap olacaktır.

Genelleştirmeler

Çap kavramının çember, daire ya da küre gibi geometrik nesneler üzerinde verilen tanımı herhangi Öklid uzayında yer alan bir yuvar ya da daha genel olarak uzaklık kavramının karşılığının bulunduğu metrik uzaylardaki kümeler için genelleştirilebilir. Eğer uzaklık kavramının olduğu uzayda bir küme verilmişse, çap bu kümedeki herhangi iki elemanın birbirine uzaklıklarından oluşan kümenin en küçük üst sınırı olarak tanımlanır.

Örneğin, Kartezyen düzlemde merkezi başnoktada ve yarıçapı 1 olan bir kapalı dairenin içindeki noktaların birbirine olan uzaklıklarının kümesi $[0,2]$ olacaktır. Bu durumda, kümenin en küçük üst sınırı 2dir. Eğer daire kapalı olmak yerine açık daire alınsaydı, bu sefer dairenin içindeki noktaların birbirine olan uzaklıklarının kümesi $[0,2)$ olacaktı. Ancak, bu kümenin de en küçük üst sınırı 2dir. Her iki durumda da çap beklendiği gibi 2 olarak belirlendi.

Diğer taraftan tam orta noktası başnoktada yer alan ve bir kenarı 2 birim olan bir karenin çapı, burada verilen tanıma göre $2{\sqrt {2}}$ olacaktır. Gerçekten de, birbirine çapraz konumda olan iki köşe arasındaki uzaklık Pisagor teoremi yardımıyla ${\sqrt {2^{2}+2^{2}}}={\sqrt {8}}={\sqrt {2^{2}\times 2}}=2{\sqrt {2}}$ olarak hesaplanır.

Çap kavramının burada bahsedilen anlam genelleştirmesinden farklı olarak değişik anlamlar yüklendiği durumlar da vardır. Örneğin herhangi bir koni kesitinde koninin merkezinden geçen herhangi bir kirişe de çap denilir. Ancak, bu tanım altında çap, doğru parçaları anlamında, uzunlukları birbirine eşit olmayan doğru parçaları olacaktır. Bir elipsin çaplarından en önemlileri elipsin odak noktalarından geçen ve en uzun kiriş olma özelliğine sahip olan ve asal eksenle örtüşen kiriş olan büyük eksendir. Diğeri ise, elipsin odak noktalarını birleştiren doğru parçasını hem dik kesip hem de tam ikiye bölen ve yedek eksenle örtüşen kiriş olan küçük eksendir.

Bir çemberin çapı daha önce tanımlandığı gibi yarıçapının tam iki katıdır. Ancak bu yalnızca bir çember için ve yalnızca Öklid metriğinde doğrudur. Jung teoremi, çapı yarıçapla ilişkilendiren daha genel eşitsizlikler vermektedir.

Ayrıca bakınız

• Teğet
• Jung teoremi
• Eratosthenes, Dünyanın çapını M.Ö