Çift merkezi

Astronomide çift merkezi (barisenter, yalpalama merkezi, kütle merkezi veya ağırlık merkezi; Eski Yunanca βαρύς (barús) 'ağır' ve κέντρον (kéntron) 'merkez')^[1] birbirinin yörüngesinde dönen iki veya daha fazla cismin kütle merkezidir ve cisimlerin etrafında döndüğü noktadır. Çift merkez fiziksel bir nesne değil, dinamik bir noktadır. Astronomi ve astrofizik gibi alanlarda önemli bir kavramdır. Bir cismin kütle merkezinden çift merkeze olan mesafesi iki cisim problemi olarak hesaplanabilir.

Çift merkez animasyonları

90 Antiope asteroid sistemi gibi benzer kütleye sahip iki cisim

Plüton ve Charon gibi kütleleri biraz farklı iki cisim

Dünya ve Ay gibi kütleleri arasında önemli fark olan iki cisim

Güneş ve Dünya gibi kütleleri arasında aşırı fark olan iki cisim

Aynı kütleye sahip iki cismin eksantrik eliptik yörüngeleri, ikili yıldızlar için yaygındır

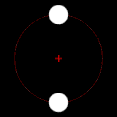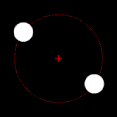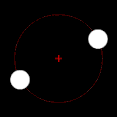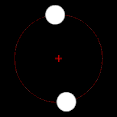
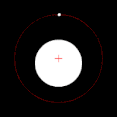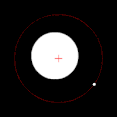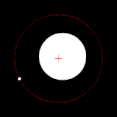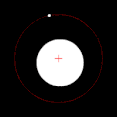
Yörüngede dönen iki cisimden biri diğerinden çok daha büyükse ve cisimler birbirine nispeten yakınsa, çift merkez tipik olarak daha büyük kütleli cismin içinde yer alacaktır. Bu durumda, iki cisim aralarında bir nokta etrafında dönüyor gibi görünmek yerine, daha az kütleli cisim daha kütleli cismin etrafında dönüyor gibi görünürken, daha kütleli cismin hafifçe yalpaladığı gözlemlenebilir. Bu durum, Dünya-Ay sistemi için geçerlidir; Dünya'nın merkezinden ortalama 4.671 km (2.902 mi) uzakta bulunan bu merkez, Dünya'nın 6.378 km (3.963 mi) olan yarıçapının %75'ine denk gelmektedir. İki cisim benzer kütlelere sahip olduğunda, çift merkez genellikle cisimlerin aralarındaki bir noktada yer alacak ve her iki cisim de onun etrafında dönecektir. Bu durum Plüton ve Plüton'un doğal uydularından biri olan Charon'un yanı sıra birçok ikili asteroit ve ikili yıldız için de geçerlidir. Daha az kütleli nesne uzakta olduğunda, çift merkez daha kütleli nesnenin dışında yer alabilir. Jüpiter ve Güneş için durum böyledir; Güneş Jüpiter'den bin kat daha büyük olmasına rağmen, aralarındaki nispeten büyük mesafe nedeniyle çift merkezleri Güneş'in biraz dışındadır.^[2]

Astronomide çift merkezli koordinatlar, kökeni belirli iki veya daha fazla cismin merkez noktası olan ve dönmeyen konumlardır. Uluslararası Göksel Referans Sistemi (ICRS), Güneş Sistemi'nin çift merkezini merkez alan çift merkezli bir koordinat sistemidir.

İki cisim problemi

Çift merkez, her cismin eliptik yörüngesinin odaklarından biridir. Bu, astronomi ve astrofizik alanlarında önemli bir kavramdır. İki cisimli basit bir durumda, birincil merkezden çift merkeze olan uzaklık, r1, şu şekilde hesaplanır:

$r_{1}=a\cdot {\frac {m_{2}}{m_{1}+m_{2}}}={\frac {a}{1+{\frac {m_{1}}{m_{2}}}}}$

bu formülde:

r ₁ ana cismin merkezinden ağırlık merkezine olan mesafedir
a iki cismin merkezleri arasındaki mesafedir
m ₁ ve m ₂ iki cismin kütleleridir.

İkincil yörüngenin yarı büyük ekseni r ₂, r₂ = a − r₁ formülü ile hesaplanır.

Çift merkez daha büyük kütleli cismin içinde yer aldığında, bu cisim fark edilebilir bir yörüngeyi takip etmek yerine "yalpalıyor" gibi görünecektir.

Birincil-ikincil örnekler

Aşağıdaki tabloda Güneş Sisteminden bazı örnekler verilmiştir. Rakamlar üç özel işarete yuvarlanarak verilmiştir. "Birincil" ve "ikincil" terimleri, ilgili aktörler arasında ayrım yapmak için kullanılmıştır; büyük olan birincil, küçük olan ise ikincil aktördür.

m₁ Dünya kütlelerindeki birincil kütlenin kütlesi (M_🜨)
m₂ Dünya kütlelerindeki ikincil kütlenin kütlesi (M_🜨)
a (km) iki cismin merkezleri arasındaki ortalama yörünge mesafesidir
r₁ (km) birincilin merkezinden çift merkeze olan mesafedir
R₁ (km) birincil yarıçapıdır
r₁/R₁ birden küçük bir değer, çift merkezinin birincilin içinde olduğu anlamına gelir

**Birincil-İkincil örnekler**
Birincil	m₁ (`M`_🜨)	İkincil	m₂ (`M`_🜨)	a (km)	r₁ (km)	R₁ (km)	r₁/R₁
Dünya	1	Ay	0,0123	384.000	4.670^[3]	6.380	0,732^[a]
Plüton	0,0021	Charon	0,000254 (0,121 M_♇)	19.600	2.110	1.150	1,83^[b]
Güneş	333.000	Dünya	1	150.000.000 (1 AU)	449	696.000	0,000646^[c]
Güneş	333.000	Jüpiter	318 (0,000955 `M`_☉)	778.000.000 (5,20 AU)	742.000	696.000	1,07^[5]^[d]
Güneş	333.000	Satürn	95,2	1.430.000.000 (9,58 AU)	409.000	696.000	0,588

^ Dünya'nın gözle görülür bir "sallantısı" vardır. Ayrıca bkz. Gelgit.
^ Plüton ve Charon bazen ikili bir sistem olarak kabul edilir çünkü çift merkezleri her iki cismin de içinde yer almaz.^[4]
^ Güneş'in yalpalaması zorlukla algılanabilir.
^ Güneş, yüzeyinin hemen üzerindeki bir ağırlık merkezinin etrafında döner.^[6]

Güneş örneği

Güneş Sistemi'nin ağırlık merkezinin Güneş'e göre hareketi

Eğer halihazırda geçerli olan m₁ ≫ m₂ durumunda oranr₁/R₁'dir :

${\frac {a}{R_{1}}}\cdot {\frac {m_{2}}{m_{1}}}.$

Bu nedenle, Güneş-gezegen sisteminin çift merkezi yalnızca aşağıda hesaplanmakta olan durumlarda Güneş'in dışında olacaktır:

${a \over R_{\odot }}\cdot {m_{\mathrm {planet} } \over m_{\odot }}>1\;\Rightarrow \;{a\cdot m_{\mathrm {planet} }}>{R_{\odot }\cdot m_{\odot }}\approx 2.3\times 10^{11}\;m_{\oplus }\;{\mbox{km}}\approx 1530\;m_{\oplus }\;{\mbox{AU}}$

— yani gezegenin kütlesinin büyük ve Güneş'e olan mesafesinin fazla olduğu durumda bu gerçekleşir..

Eğer Jüpiter Merkür'ün yörüngesine sahip olsaydı (57.900.000 km, 0,387 AU), Güneş-Jüpiter çift merkezi Güneş'in merkezinden yaklaşık 55.000 km uzakta olurdu (r₁/R₁ ≈ 0.08). Ancak Dünya Eris'in yörüngesine sahip olsaydı bile (1,02×10¹⁰ km, 68 AU), Güneş-Dünya çift merkezi yine de Güneş'in içinde olurdu (merkezden 30.000 km'nin biraz üzerinde).

Güneş'in gerçek hareketini hesaplamak için sadece dört dev gezegenin (Jüpiter, Satürn, Uranüs, Neptün) hareketlerinin dikkate alınması gerekir. Diğer tüm gezegenlerin, cüce gezegenlerin vb. katkıları ihmal edilebilir düzeydedir. Eğer dört dev gezegen Güneş'in aynı tarafında düz bir çizgi üzerinde olsalardı, birleşik kütle merkezi yaklaşık 1,17 güneş yarıçapında ya da Güneş yüzeyinden 810.000 km'nin biraz üzerinde olurdu.^[7]

Yukarıdaki hesaplamalar cisimler arasındaki ortalama mesafeye dayanmaktadır ve ortalama r1 değerini sağlamaktadır. Ancak tüm göksel yörüngeler eliptiktir ve cisimler arasındaki mesafe eksantrikliğe (e) bağlı olarak apsisler arasında değişir. Dolayısıyla, çift merkezin konumu da değişken olup, bazı sistemlerde çift merkezin bazen daha büyük cismin içinde bazen de dışında olması mümkündür. Bu durum şu hallerde ortaya çıkar:

${\frac {1}{1-e}}>{\frac {r_{1}}{R_{1}}}>{\frac {1}{1+e}}$

Güneş-Jüpiter sistemi e_Jüpiter = 0,0484 değeriyle birlikte yukarıdaki formüle göre 1,05<1,07<0,954 gerekliliğini sağlamamaktadır.

Göreli düzeltmeler

Klasik mekanikte (Newton kütleçekim kuramı) bu tanım hesaplamaları kolaylaştırmakta ve bilinen hiçbir soruna yol açmamaktadır. Genel görelilikte (Einstein kütleçekim kuramı), karmaşıklıklar ortaya çıkar, çünkü makul yaklaşımlar dahilinde çift merkezi tanımlamak mümkün olsa da, ilişkili koordinat sisteminin farklı konumlardaki saat hızlarının eşitsizliğini tam olarak yansıtmamaktadır. Brumberg, genel görelilikte çift merkezli koordinatların nasıl kurulacağını açıklamaktadır.^[8]

Koordinat sistemleri bir dünya zamanı, yani telemetri ile ayarlanabilen küresel bir zaman koordinatı içerir. Benzer yapıdaki münferit saatler, farklı yerçekimi potansiyellerine maruz kaldıkları ya da farklı hızlarda hareket ettikleri için bu standartla uyuşmayacaktır, bu nedenle dünya zamanı, kendi kendine yerçekimi yapan tüm sistemden çok uzakta olduğu varsayılan ideal bir saatle senkronize edilmelidir. Bu zaman standardına Barisentrik Koordinat Zamanı (TCB [sic]) adı verilir.

Bazi çift merkezli cisimlerin yörünge elemanları

Güneş Sistemi'ndeki bazı nesneler için çift merkezli salınımlı yörünge elemanları aşağıda verilmiştir.^[9]

Nesne	Yarı büyük eksen (AU'da )	Apoapsis (AU'da)	Yörünge dönemi (yıl)
C/2006 P1 (McNaught)	2.050	4.100	92.600
C/1996 B2 (Hyakutake)	1.700	3.410	70.000
C/2006 M4 (Kuğu)	1.300	2.600	47.000
(308933) 2006 SQ372	799	1.570	22.600
(87269) 2000 OO67	549	1.078	12.800
90377 Sedna	506	937	11.400
2007 TG422	501	967	11.200

Bu kadar yüksek eksantriklikteki nesneler için, çift merkezli koordinatlar belirli bir dönem için güneş merkezli koordinatlardan daha kararlıdır çünkü çift merkezli salınımlı yörünge Jüpiter'in 11,8 yıllık yörüngesinde nerede olduğundan büyük ölçüde etkilenmez.^[10]

Ayrıca bakınız

Kaynakça

^ "barycentre". Oxford English Dictionary (Çevrimiçi bas.). Oxford University Press. (Abonelik veya katılımcı kurum üyeliği gerekli.)
^ MacDougal, Douglas W. (2012). Newton's gravity: an introductory guide to the mechanics of the universe. Undergraduate lecture notes in physics. New York: Springer. ISBN 978-1-4614-5444-1.
^ "Center of Gravity - an overview". ScienceDirect Topics. 20 Nisan 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Kasım 2023. barycentre lies 1700 km below the Earth's surface
(6370 km–1700 km)
^ Kaynak hatası: Geçersiz <ref> etiketi; Olkin-2015 isimli refler için metin sağlanmadı (Bkz: Kaynak gösterme)
^ "If You Think Jupiter Orbits the Sun, You're Mistaken". HowStuffWorks (İngilizce). 9 Ağustos 2016. 3 Ekim 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Kasım 2023. The Sol-Jupiter barycenter sits 1.07 times the radius of the sun
^ Kaynak hatası: Geçersiz <ref> etiketi; NASA2005 isimli refler için metin sağlanmadı (Bkz: Kaynak gösterme)
^ Meeus, Jean (1997). Mathematical astronomy morsels. Richmond, Va: Willmann-Bell. ISBN 978-0-943396-51-4.
^ Brumberg, Victor Alexandrovič (1991). Essential relativistic celestial mechanics. Bristol Philadelphia New York: A. Hilger. ISBN 978-0-7503-0062-9.
^ Horizons çıktısı (30 Ocak 2011). "Barycentric Osculating Orbital Elements for 2007 TG422". 28 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ocak 2011. (Select Ephemeris Type:Elements and Center:@0)
^ Kaib, Nathan A.; Becker, Andrew C.; Jones, R. Lynne; Puckett, Andrew W.; Bizyaev, Dmitry; Dilday, Benjamin; Frieman, Joshua A.; Oravetz, Daniel J.; Pan, Kaike; Quinn, Thomas; Schneider, Donald P. (Mart 2009). "2006 SQ372: A LIKELY LONG-PERIOD COMET FROM THE INNER OORT CLOUD". The Astrophysical Journal (İngilizce). 695 (1): 268. doi:10.1088/0004-637X/695/1/268. ISSN 0004-637X.

[PSEx1-4] Dünya'nın gözle görülür bir "sallantısı" vardır. Ayrıca bkz. Gelgit.

[PSEx2-6] Plüton ve Charon bazen ikili bir sistem olarak kabul edilir çünkü çift merkezleri her iki cismin de içinde yer almaz.^[4]

[PSEx3-7] Güneş'in yalpalaması zorlukla algılanabilir.

[PSEx4-10] Güneş, yüzeyinin hemen üzerindeki bir ağırlık merkezinin etrafında döner.^[6]

[1] "barycentre". Oxford English Dictionary (Çevrimiçi bas.). Oxford University Press. (Abonelik veya katılımcı kurum üyeliği gerekli.)

[2] MacDougal, Douglas W. (2012). Newton's gravity: an introductory guide to the mechanics of the universe. Undergraduate lecture notes in physics. New York: Springer. ISBN 978-1-4614-5444-1.

[3] "Center of Gravity - an overview". ScienceDirect Topics. 20 Nisan 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Kasım 2023. barycentre lies 1700 km below the Earth's surface
(6370 km–1700 km)

[Olkin-2015-5] Kaynak hatası: Geçersiz <ref> etiketi; Olkin-2015 isimli refler için metin sağlanmadı (Bkz: Kaynak gösterme)

[8] "If You Think Jupiter Orbits the Sun, You're Mistaken". HowStuffWorks (İngilizce). 9 Ağustos 2016. 3 Ekim 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Kasım 2023. The Sol-Jupiter barycenter sits 1.07 times the radius of the sun

[NASA2005-9] Kaynak hatası: Geçersiz <ref> etiketi; NASA2005 isimli refler için metin sağlanmadı (Bkz: Kaynak gösterme)

[11] Meeus, Jean (1997). Mathematical astronomy morsels. Richmond, Va: Willmann-Bell. ISBN 978-0-943396-51-4.

[12] Brumberg, Victor Alexandrovič (1991). Essential relativistic celestial mechanics. Bristol Philadelphia New York: A. Hilger. ISBN 978-0-7503-0062-9.

[barycenter-13] Horizons çıktısı (30 Ocak 2011). "Barycentric Osculating Orbital Elements for 2007 TG422". 28 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ocak 2011. (Select Ephemeris Type:Elements and Center:@0)

[14] Kaib, Nathan A.; Becker, Andrew C.; Jones, R. Lynne; Puckett, Andrew W.; Bizyaev, Dmitry; Dilday, Benjamin; Frieman, Joshua A.; Oravetz, Daniel J.; Pan, Kaike; Quinn, Thomas; Schneider, Donald P. (Mart 2009). "2006 SQ372: A LIKELY LONG-PERIOD COMET FROM THE INNER OORT CLOUD". The Astrophysical Journal (İngilizce). 695 (1): 268. doi:10.1088/0004-637X/695/1/268. ISSN 0004-637X.

[1]

[2]

[3]

[a]

[b]

[c]

[5]

[d]

[4]

[6]

[7]

[8]

[9]

[10]