Taylor teoremi

Kalkülüste Taylor teoremi, türevi tanımlı bir işleve bir nokta çevresinde, katsayıları yalnızca işlevin o noktadaki türevine bağlı olan polinomlar cinsinden bir yaklaştırma dizisi üreten bir sonuçtur. Teorem, yaklaştırma hesaplamalarındaki hata payına ilişkin kesin sonuçlar da verebilmektedir. Brook Taylor adlı matematikçinin 1712 yılında yaptığı çalışmalarından ötürü ismi bu şekilde anılan teoremin aslında bundan 41 yıl önce (1671 yılında) James Gregory tarafından bulunduğu bilinmektedir.

Orijin çevresinde $y=e^{x}$ üstel işlevi (sürekli kırmızı çizgi) ve karşılık gelen dördüncü dereceden Taylor polinomu (kesikli yeşil çizgi)

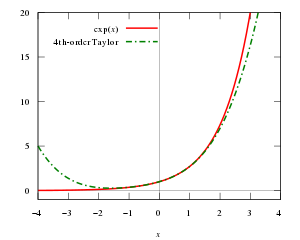
Taylor teoremine göre k defa türevlenebilir bir fonksiyona, verilen bir noktada yakınsayan k derece polinoma Taylor polinomu denir. Birinci derece Taylor polinomu doğrusal yaklaşım (İngilizce: linear approximation) olarak, ikinci derece Taylor polinomuysa karesel yaklaşım (İngilizce: quadratic approximation) olarak da bilinir.

Giriş

f(x) = e^x (mavi) ve onun x=0 noktasındaki doğrusal yaklaşımı P₁(x) = 1 + x (kırmızı).

Eğer f(x) gerçel fonksiyonu x = a noktasında türevlenebilir ise, bu noktada doğrusal yaklaşımı var demektir. Dolayısıyla, aşağıdaki gibi bir h₁(x) fonksiyonu vardır:

$f(x)=f(a)+f'(a)(x-a)+h_{1}(x)(x-a),\quad \lim _{x\to a}h_{1}(x)=0.$

Burada

$P_{1}(x)=f(a)+f'(a)(x-a)$

terimi, f(x)'in x = a noktasındaki doğrusal yaklaşımıdır ve grafiği f(x)'e teğettir. Yaklaşım hatası aşağıdaki gibi hesaplanır:

$R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(x-a).$

x değişkeni a değerine yaklaştıkça, bu hata $f'(a)(x{-}a)$'ten daha hızlı şekilde sıfıra yaklaşır, dolayısıyla $f(x)\approx P_{1}(x)$ yaklaşımı kullanışlıdır.

f(x) = e^x (mavi) e onun x=0 noktasındaki karesel yaklaşımı P₂(x) = 1 + x + x²/2 (kırmızı). Hata payındaki düşüşe dikkat ediniz.

Daha iyi bir tahmin bulmak için f(x)'e bir karesel polinom yaklaştırabiliriz:

$P_{2}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}.$

f(x)'in x = a'da yalnız bir türevini eşleştirmek yerine, hem birinci hem de ikinci türevlerini bu polinomla temsil edebiliriz.

Taylor teoremine göre, karesel yaklaşım x=a'nın yeterince küçük bir mahalinde doğrusal yaklaşımdan daha isabetli bir tahmin sunar. Aşağıdaki yaklaşıma göre

$f(x)=P_{2}(x)+h_{2}(x)(x-a)^{2},\quad \lim _{x\to a}h_{2}(x)=0.$

Hata değeri

$R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(x-a)^{2},$

x değişkeni a değerine yaklaştıkça, $(x-a)^{2}$'den daha hızlı şekilde sıfıra yaklaşır.

Bu şekilde daha üst dereceden polinomlar kullanarak daha doğru bir yaklaşım elde edilebilir. Bunun sebebi, yaklaşım polinomunun verilen noktada f'nin daha üst dereceden türevleriyle eşleşmesidir.

Genel olarak, x a'ya yaklaşırken, k dereceden bir yaklaşım polinomunun hatasının sıfıra yaklaşma hızı, $(x-a)^{k}$'nin yaklaşma hızından daha fazladır. Ancak, sonsuz derecede türevlenebilir olsa dahi isabetli bir yaklaşımı bulunmayan fonksiyonlar da vardır. Bu fonksiyonların x = a'da analitik olmadığı söylenir. Yani fonksiyon bu nokta ve çevresinde türevleriyle belirlenemez.

Tek değişkenli Taylor teoremi

Taylor teoreminin en basit halinin açık ifadesi şöyledir:

k ≥ 1 bir tam sayı ve f : R → R a ∈ R noktasında k defa türevlenebilir bir fonksiyon olsun. Öyleyse aşağıdaki tanıma sahip bir h_k : R → R fonksiyonu vardır:

$f(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},$

ve

$\lim _{x\to a}h_{k}(x)=0.$

Buna kalanın Peano biçimi denir.

Taylor teoremindeki polinom f fonksiyonunun a noktasındaki k dereceden Taylor polinomudur:

$P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}$

Taylor polinomu biricik "asimtotik en uygun" polinomdur. Yani, aşağıdaki gibi h_k : R → R fonksiyonu ve k dereceden polinom p varsa

$f(x)=p(x)+h_{k}(x)(x-a)^{k},\quad \lim _{x\to a}h_{k}(x)=0,$

o halde p = P_k'dir. Taylor teoremi kalan terim'in asimptotik davranışını ifade eder:

$R_{k}(x)=f(x)-P_{k}(x),$

Bu terim, f bir Taylor polinomuyla tahminlendiğindeki yaklaşım hatasıdır.

Ayrıca bakınız

• Taylor dizisi
• Doğrusal yaklaştırma
• Üs dizisi
• Laurent dizisi – Taylor dizisinin tekil noktalara sahip işlevlere uyarlanmış biçimi

Dış bağlantılar

• Taylor Dizisinin Kosinüs Yaklaştırması 4 Ocak 2010 tarihinde Wayback Machine sitesinde arşivlendi.
• Trigonometrik Taylor Açılımı10 Kasım 2007 tarihinde Wayback Machine sitesinde arşivlendi. etkileşimli görsel sunum
• Taylor Dizisi, Yeniden5 Haziran 2009 tarihinde Wayback Machine sitesinde arşivlendi., Bütüncül Sayısal Yöntemler Enstitüsü6 Eylül 2006 tarihinde Wayback Machine sitesinde arşivlendi.